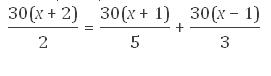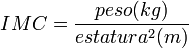Blog de un estudiante de 4º de ESO del IES Celia Viñas. Haz del mundo un lugar mejor. Sin fracaso no hay éxito. Don't let little minds tell you that your dreams are too big.
jueves, 1 de diciembre de 2011
martes, 22 de noviembre de 2011
miércoles, 16 de noviembre de 2011
jueves, 10 de noviembre de 2011
martes, 8 de noviembre de 2011
lunes, 7 de noviembre de 2011
miércoles, 2 de noviembre de 2011
jueves, 27 de octubre de 2011
martes, 25 de octubre de 2011
lunes, 24 de octubre de 2011
martes, 18 de octubre de 2011
domingo, 16 de octubre de 2011
sábado, 8 de octubre de 2011
domingo, 25 de septiembre de 2011
domingo, 12 de junio de 2011
jueves, 26 de mayo de 2011
Instrumentos para estudiar a los seres vivos
La forma de pensar a cambiado a lo largo de los siglos y de los años, fundamentalmente, por la aparición de instrumentos que nos hicieron cambiar nuestra forma de pensar, que solo teníamos por la percepción de los sentidos, pero que con esos instrumentos, nos ayudaron a ir más allá de lo que captamos.
En estas diapositivas, nombro para que nos ha servido estos instrumentos y como uno de ellos, el microscopio, nos hizo cambiar radicalmente nuestra manera de ver el mundo.
martes, 24 de mayo de 2011
domingo, 22 de mayo de 2011
viernes, 20 de mayo de 2011
Ecuaciones de primer grado. ¿Cómo se resuelven?
En este post, dedicado a todos los alumnos de 1º de ESO que están dando este tema, o los que están por darlo, explico qué es una ecuación, y cómo resolverla, aplicando diferentes procedimientos que voy a explicar.
Espero que os ayude :)
Primero, vamos a empezar a definir que es una ecuación, pero con mis palabras:
 Una ECUACIÓN son dos expresiones algebraicas con dos miembros, en la que se tiene que cumplir una igualdad averiguando las incógnitas, que es el nombre que reciben las letras o la parte literal de la ecuación.
Una ECUACIÓN son dos expresiones algebraicas con dos miembros, en la que se tiene que cumplir una igualdad averiguando las incógnitas, que es el nombre que reciben las letras o la parte literal de la ecuación.Es como una balanza en la que para averiguar las incógnitas hay que equilibrar la balanza, para que haya el mismo peso en ambos lados de ella.
Ejemplos:
x + 6 = 31 5 + x = 31
2x + 1 = 6x + 2 2
5(6x-3) = 6(x + 5)- x 2 + 3x = 18
Este año hemos dado las ecuaciones de primer grado, o lo que es lo mismo, ecuaciones de exponente 1.
Hay 2 procedimientos básicos para resolver 2 tipos de ecuaciones simples: La Regla de la Suma y la Regla del Producto.
Ambas consisten en equilibrar la balanza, y voy a explicarlas a continuación:
En todas las ecuaciones que os encontréis, el objetivo va a ser despejar a la x, es decir, dejarla sola para hallar su valor y poder hallar la ecuación.
En la Regla de la suma el objetivo es el siguiente, poniendo un ejemplo sencillo:
x + 6 = 18.
1º Restamos el 6 que nos "molesta" para despejar la x: x + 6 - 6
2º Pasamos la resta al otro miembro: 18 - 6
3º Realizamos las cuentas y sale el resultado: x = 12
En este caso debemos dejar a la x sola pero, para eso, hay que restar 6; pero entonces la balanza quedaría desequilibrada, así que tendríamos que restar al otro miembro también 6. Por eso decimos que una suma pasa al otro miembro restando, no por arte de magia.
Ahora, teniendo en cuenta este ejemplo, con las restas será al revés, para hacer desparecer el número al restar habrá que sumarlo. Vamos a hacer el mismo ejemplo pero restando:
x - 6 = 18
1º Sumamos el x que nos molesta. x - 6 + 6
2º Pasamos la suma al otro miembro: 18 + 6
3º Realizamos las cuentas y el resultado sale: x = 24.
Más ejemplos de la Regla de la Suma:
3x + 23 = 2x + 59
1º 3x - 2x + 23 - 23 = 59 - 23 (Este paso lo hacemos ya directamente)
2º x = 36
24 + x - 6 = 50 + 6
1º 24 - 24 + x - 6 + 6 = 50 + 6 - 24 + 6
2º x = 38
x + 7 = 7 + 12
1º x + 7 - 7 = 7 + 12 - 7
2º x = 12
Regla del Producto: Esta regla consiste en lo mismo que en la de la suma, solo que con multiplicaciones y divisiones, con la finalidad de despejar a la x. A continuación pongo un par de ejemplos para resolver con la regla del producto, con multiplicación y división:
3x = 24
4
1º Multiplicamos el denominador por 4 en el primer miembro, para quitar el denominador, pero hay que hacerlo en los 2 miembros 3x x 4 = 24 x 4
4
2º Ahora ya tenemos un resultado, pero queremos saber el valor de una x, no de 3. 3x = 96
3º Dividimos 3 entre 3 para obtener una x, y lo hacemos en el otro miembro para hallar su valor y compensar la balanza.3x = 96 x = 32
3 3
Otro ejemplo más sencillo aún:
4x = 44
1º Dividimos entre 4 para hallar el valor de una x en los dos miembros:
4x = 44 x = 11
4 4
Ahora vamos a dar la Resolución de Ecuaciones, o lo que es lo msimo, la regla práctica para resolverlas.
Vamos a dar como se resuelven ecuaciones con paréntesis y con denominadores, y mixtas. Vamos a empezar por los paréntesis:
Para resolver ecuaciones con paréntesis, seguimos el siguiente procedimiento:
1º Suprimimos los paréntesis, y para ello, hay que aplicar la propiedad distributiva.
2º Aplicamos la regla de la suma
3º Aplicamos la regla del producto
Ejemplos:
3(x + 6) + 5(2 - x) = 10 - 4(6 + 2x).
1º Suprimimos paréntesis:
3x + 18 + 10 - 5x = 10 - 24 - 8x
2º Aplicamos regla de la suma: (dejamso x en un lado y los números en otro)
3x - 5x + 8x = 10 - 24 - 18 - 10
6x = -42
3º Aplicamos la regla del producto:
6x = -42 x= -7
6x 6
Voy a poner algunas ecuaciones más de este tipo, pero ya sin explicar el proceso. ¡¡Intentar hacerlos a la misma vez y comprobar si lo tenéis bien!!
3(x - 7) = 5(x-1) - 4x
1º 3x - 21 = 5x - 5 - 4x
2º 3x- 5x + 4x = -5 + 21
3º 2x = 16 x = 8
Ahora, ya que hemos hecho ecuaciones con paréntesis, vamos a aprender hacer ecuaciones con denominadores. Los pasos son muy sencillos, y son los siguientes:
1º Suprimimos los paréntesis antes de los denominadores si hay
2º Eliminamos los denominadores.
Para ello, debemos encontrar el mcm de todos los denominadores, y cuando lo tengamos dividimos ese número entre el denominador de cada uno y lo multiplicamos por el de arriba
3º Ponemos la ecuación resultante pero suprimiendo los denominadores
4º Aplicamos la regla de la suma y del producto
Voy a poner algunos ejemplos:
1º Paréntesis
30x + 60 = 30x + 30 + 30x - 30
2 5 3
2º Eliminamos los denominadores (mcm)
450x + 900 = 180x + 180 + 300x - 300
30 30 30
3º Ecuación sin denominadores
450x + 900 = 180x + 180 + 300x - 300
4º Regla de la suma y del producto
450x - 180x - 300 = 180 - 300 - 900
270x = -1020
270x = -1020
270 270
x = -1020
270

Bueno, ya os he enseñado los procedimientos para hacer una ecuación. Ahora, ¡¡EN MARCHA!!
jueves, 19 de mayo de 2011
Las rocas y minerales de la geosfera, y la organización en capas de ésta
Como bien dice el título de este post, esta presentación habla sobre la litosfera (llamada también geosfera), y de sus capas. Además, explico el concepto de roca, mineral, y cristal, los cuales son muy importantes.
Oímos constantemente la palabra roca, mineral y cristal, y lo primero que pensamos de roca es algo que esté en el suelo y duro, cuando oímos mineral pensamos: lo que lleva el agua... , y cuando pensamos en cristales pensamos en la ventana. Pues estamos muy equivocados.
Ya explico en mi presentación cada concepto pero, además, lo voy a explicar aquí, porque es muy importante.
Las rocas son mezclas, ya que son sustancias formadas por varios minerales.
Los minerales son sustancias puras, las cuales tienen los átomos ordenados, y esas sustancias son inorgánicas.
Por último, los cristales son sustancias en estado sólido que tienen los átomos ordenados.
A continuación expongo mi entrada de diapositivas, la cual espero que os guste. :)
jueves, 12 de mayo de 2011
Separación de sustancias y su aplicación cotidiana
Seguro que os sabéis de memorieta cuales son los métodos de separación de sustancias: filtración, tamizado, decantación... Pero, la cuestión es, ¿sabéis realmente su importancia?
Pues es más importante de lo que creeis. Sin separar sustancias no tendrías ese rico café que te tomas todas las mañanas(para los que beben café), no conducirías el coche para ir al instituto, colegio, trabajo..., ni la sal que hace que no esté sosa la comida y que te la puedas comer en condiciones.
Hay un montón de usos que le podemos dar a la separación de sustancias, pero en esta presentación voy a tratar sobre las propiedades de las sustancias y los métodos de separación de sustancias, aplicando cada método con una acción de la vida cotidiana.
Espero que os sirva de ayuda, y cualquier fallo que consideréis que puedo corregir, no dudéis en comentar!! :)
lunes, 9 de mayo de 2011
El ciclo del agua y su relacion con el balance energetico del planeta
El ciclo del agua es IMPORTANTÍSIMO. Nos parece una cosa sencilla, que a simple vista puede parecer: El agua se evapora, se condensa y cae en forma de lluvia, y así de sencillo. No, el ciclo del agua es algo más que eso, el ciclo del agua es REPARTIR ENERGÍA, nunca mejor dicho.
Y es que es verdad, si las moléculas de agua se mueven, y van de un sitio a otro, hacen que circule la energía, que no esté la energía parada, estancada.
Y además, transportar energía es algo más que erosionar, transportar y sedimentar, es dar a los seres vivos el elemento esencias que se obtiene en el ciclo, el agua, que pasa a los seres vivos y nos permite llevar a cabo las funciones de nuestro cuerpo.
Además, el ciclo del agua pasa por nosotros, en nuestros cuerpos (al beber un vaso de agua, por ejemplo), y sale de nuevo al orinar...
A continuación os presento mis diapositivas, las cuales espero que os sirvan :)
Existencia de la biosfera
Todos hemos oído hablar de la biosfera. Pero no nos queda claro que es. La biosfera es el elemento de la que formamos todos los seres vivos que habitamos la Tierra.
Sí, estamos en la biosfera y en relación con otros medios. Con la atmósfera, respirando el aire que se encuentra en ella. Con la hidrosfera, utilizando el agua que se encuentra en ella, y la geosfera (nuestros pies están pisando ahora mismo la geosfera, claro, si los tenéis en el suelo, jeje)
A continuación expongo esta presentación de diapositivas, que explica que es la biosfera, además, explica los ecosistemas y la cadena alimentaria.
jueves, 14 de abril de 2011
Expresiones algebraicas, ¿¡Quéeeeeeeeeee!?
Bueno, lo primero, espero que no sepáis lo que es una expresión algebraica, porque si no, ¿para qué estáis leyendo esto?
En la clase de 1º de Eso del IES CELIA VIÑAS, estamos dando un tema nuevo para nosotros, el lenguaje algebraico y las ecuaciones, y nuestro profesor nos ha pedido que realicemos este post explicando que es una expresión algebraica.
Antes de explicaros que es una expresión algebraica, debéis saber que el lenguaje algebraico es:
El lenguaje de las matemáticas, el cual se utiliza para pasar procedimientos cotidinaos al lenguaje matemático, en el que se utilizan letras del alfabeto, incluso del alfabeto griego (número pi)
Después de esto, mejor vayamos al grano, ¿vale?
Las expresiones algebraicas cuentan con dos partes:
Las expresiones algebraicas se utilizan casi sin darnos cuenta constantemente en la vida cotidiana, algunos ejemplos pueden ser:
¿Sabéis que el buscador más famoso del mundo, Google, es una expresión algebraica o ecuación? Sí, es una ecuación, que resuelve más de 500 millones de variables y más de 2000 millones de términos. Además, a parte de buscar las palabras solicitadas, las evalúa según la importancia.
La ecuación es: E = mc2, que indica la equivalencia entre masa y energía.
En la clase de 1º de Eso del IES CELIA VIÑAS, estamos dando un tema nuevo para nosotros, el lenguaje algebraico y las ecuaciones, y nuestro profesor nos ha pedido que realicemos este post explicando que es una expresión algebraica.
Antes de explicaros que es una expresión algebraica, debéis saber que el lenguaje algebraico es:
El lenguaje de las matemáticas, el cual se utiliza para pasar procedimientos cotidinaos al lenguaje matemático, en el que se utilizan letras del alfabeto, incluso del alfabeto griego (número pi)
Una expresión algebraica es un conjunto o combinación de letras y números que están unidos por operaciones básicas (sumar, restar, dividir, multiplicar, potencias, fracciones).
Las expresiones algebraicas cuentan con dos partes:
- El coeficiente
- La parte literal.
El coeficiente expresa el número, y la parte literal, como bien dice, las letras.
Las expresiones algebraicas se utilizan casi sin darnos cuenta constantemente en la vida cotidiana, algunos ejemplos pueden ser:
El índice de masa corporal (IMC) =
Hallar el área de un campo de fútbol (Rectángulo) =
La regla del tres =
Área del cuadrado (lado por lado) = x2
Área del círculo =
La densidad =
m (Masa)/ v (Volumen) = d (Densidad)
Porcentajes=
a / b = c / 100
Área del triángulo=
A = bxh / 2
Y un montón de expresiones más...
Bueno, voy a explicaros un par de curiosidades sobre las expresiones algebraicas....
¿Sabéis que el buscador más famoso del mundo, Google, es una expresión algebraica o ecuación? Sí, es una ecuación, que resuelve más de 500 millones de variables y más de 2000 millones de términos. Además, a parte de buscar las palabras solicitadas, las evalúa según la importancia.
Otra cosa, ¿Sabéis que famosa ecuación escribió Enstein? Pues escribió la ecuación más famosa de la historia, la ecuaciónd e la relatividad, la cual hizo en 1905.
martes, 12 de abril de 2011
La materia en relación con la constitución del Universo y la Tierra:
Como sabéis, el Universo está formado por materia, casi todo está formado por materia, claro, todo aquello que podemos tocar y ocupa un lugar. Pero, ¿sabemos de dónde viene el agua que recorre nuestro cuerpo, el cristal del que está hecho nuestras ventanas? Además, ¿sabemos de dónde viene la energía que está actualmente en la Tierra?
Si te interesa, te animo a que visites mi presentación de diapositivas:
Agua como agente del clima, del paisaje y de la biosfera
Todos sabemos que el agua es un elemento indispensable para la vida, como comentaba en el post de Qué es el agua y cómo se comporta como sustancia. Ahora, sin embargo, vamos a ver sus utilidades en el paisaje, en el clima y la biosfera, como explico las díapositivas siguientes:
La célula como unidad de vida
Seguramente sabéis, o habréis oído que es una célula. Seguramente sabéis que es un ser vivo microscópico, pero, su definición más sencilla es: una gota de agua atrapada. Sí, porque en su interior hay orden y mucha energía, y fuera hay poca energía, y las moléculas están lo más desordenadas posibles.
Si os interesa este tema, no dudéis en ver mi presentación de diapositivas, en la cual explico lo esencial sobre ella:
Espero que os haya gustado! :) COMENTAR!!!!!
lunes, 11 de abril de 2011
Qué es el agua y cómo se comporta como sustancia
Seguro que todos habéis oído hablar del agua, pero, ¿sabéis de qué está compuesta, como nos afecta en enfermedades, que le pasa al agua cuando está contaminada, y qué funciones realiza en lso seres vivos?
Pasaros por mi presentación de diapositivas donde explico sobre esta rara sustancia:
Espero que os ayude! :)
martes, 15 de marzo de 2011
La próxima vez analiza el chuletón...
Bueno, como seguramente sabéis, al famoso ciclista Alberto Contador, el ciclista ganador del Tour de Francia, se sometió a una prueba de dopaje. Lo malo es que dio positivo, sí, para la pena de nuestro pobre ciclista, ¡y para todos los españoles!
Pero, ¿sabéis cuánto dio el aparato que se había dopado? Pues dio exactamente 50 picogramos, que es como decir 000 000 000 005 gramos por ml. Para que os hagáis una idea, para tomar esa cantidad habría que coger un mililitro, y partirlo en mil millones de partes, y de esas partes, coger 5. En forma de fracción: 5 / 1 000 000 000
Hombre, hay que ser muy preciso para meterse esa cantidad, porque coger 5 partes de mil millones... ¡VAYA TELA!
Y es que al pobre Contador se la han montado gorda. Sí, ha dado positivo al dopaje, pero esa sustancia, el clombuterol, se utiliza para engordar a los animales, y algunos no lo pueden eliminar por completo. Vamos, Contador, que la próxima vez que te comas un buen chuletón, con sus patatitas al horno, sus verduritas... ¡ANALIZALÓ! No veo justo que por esa pequeña cantidad, lo sancionaran en el Tour. A ver, yo confío en su teoría, yo no creo que haya llegado a lo más alto por doparse, si no, sería una decepción para los españoles.
A ver, las leyes siempre han sancionado a quien se dopara, diera lo que diera la máquina (antigüamente solo detectaba si se había dopado, o no, pero con medidas mucho más grandes, y diera lo que dieran lo sancionaban) Pero, yo creo que a la vez que evoluciona la tecnología, tienen que evolucionar las leyes, hacerse más flexibles... Puf...
Yo, si fuera él, no me pondría a analizar cada chuletón o carne que pudiera contener clombuterol, la culpa, en vez de echársela a él, se las podríais echar a los que dieron esa sustancia a los animales, ellos si son los que se merecen la sanción... Bueno, a fin de cuentas, la alegría es que le han retirado la sanción.. ¡¡MENOS MAL!!
Bueno, para que os enteréis mejor, os dejo este enlace del Marca:
http://www.marca.com/2010/09/30/ciclismo/1285802253.html
Pero, ¿sabéis cuánto dio el aparato que se había dopado? Pues dio exactamente 50 picogramos, que es como decir 000 000 000 005 gramos por ml. Para que os hagáis una idea, para tomar esa cantidad habría que coger un mililitro, y partirlo en mil millones de partes, y de esas partes, coger 5. En forma de fracción: 5 / 1 000 000 000
Hombre, hay que ser muy preciso para meterse esa cantidad, porque coger 5 partes de mil millones... ¡VAYA TELA!
Y es que al pobre Contador se la han montado gorda. Sí, ha dado positivo al dopaje, pero esa sustancia, el clombuterol, se utiliza para engordar a los animales, y algunos no lo pueden eliminar por completo. Vamos, Contador, que la próxima vez que te comas un buen chuletón, con sus patatitas al horno, sus verduritas... ¡ANALIZALÓ! No veo justo que por esa pequeña cantidad, lo sancionaran en el Tour. A ver, yo confío en su teoría, yo no creo que haya llegado a lo más alto por doparse, si no, sería una decepción para los españoles.
A ver, las leyes siempre han sancionado a quien se dopara, diera lo que diera la máquina (antigüamente solo detectaba si se había dopado, o no, pero con medidas mucho más grandes, y diera lo que dieran lo sancionaban) Pero, yo creo que a la vez que evoluciona la tecnología, tienen que evolucionar las leyes, hacerse más flexibles... Puf...
Yo, si fuera él, no me pondría a analizar cada chuletón o carne que pudiera contener clombuterol, la culpa, en vez de echársela a él, se las podríais echar a los que dieron esa sustancia a los animales, ellos si son los que se merecen la sanción... Bueno, a fin de cuentas, la alegría es que le han retirado la sanción.. ¡¡MENOS MAL!!
Bueno, para que os enteréis mejor, os dejo este enlace del Marca:
http://www.marca.com/2010/09/30/ciclismo/1285802253.html
lunes, 14 de marzo de 2011
Sophie Germain y otras grandes mujeres matematicas
Hasta hace poco, la mujer ha sido un cero a la izquierda en nuestra sociedad, por lo menos en las ciencias, como son las matemaicas.
En las matematicas, el papel de las mujeres no intervenia, no porque ellas no quisieran, sino porque no se les dejaba. Sçi, vivimos en una sociedad machista, yo no comprendo el por quçe. Puede ser, como dice bien nuestro amigo Angel, nuestra "superior" fuerza que nos hace ser dominantes con las mujeres, o simplemente el hecho de que la rutina de la antiguedad hayan hecho prohibir la particicipaciçon d elas mujeres.
Estas mujeres se han esforzado mucho por intervenir en el campo de las matematicas, y muchas lo han conseguido. Una de ellas en SOphie Germain, de la cual cuento su historia resumida en estas diapositivas:
miércoles, 9 de marzo de 2011
Protoctistas, hongos, plantas y animales
No tenemos en cuenta que antes para dar lugar a la especie humana, se tuvo que empezar por algo sencillo, la célula. Después cada forma de vida adquiriría unas formas de vivir propias, que es lo que las haría características. Por eso hay varios reinos en los seres vivos, aunque en este caso vamos a hablar solo de 4:
Hongos
Protoctistas
Plantas
Animales
Echarle un vistazo a mis diapositivas, donde comento este tema ;)
domingo, 6 de marzo de 2011
¿Usamos bien los decimales? ¿En la vida cotidiana?
Las Matemáticas no solo sirven para hacer sumas y cuentas que luego no se utilizan para nada. No, si se inventaron es porque servían para algo, ¿no? Si no, seríamos tontos.
Cuando vamso al mercado, por ejemplo, cuando nos dan la cuenta a lo mejor nos dicen:
-Son 2,5 euros, y tú vas y le das 2 euros y 5 céntimos.
Es una confusión muy común en los mercados, sucede a diario. En la siguiente presentación de diapositivas os muestro una encuesta sobre este tema, para que veais como nos confundimos:
miércoles, 2 de marzo de 2011
La historia de la vida
Ya que sabemos que es estar vivo, ¿sabéis cómo surgió la vida?, ¿cuándo y qué pasó para que se produjera?
Esto es lo que explico en mis diapositivas, donde hablo sobre ello :)
Esto es lo que explico en mis diapositivas, donde hablo sobre ello :)
lunes, 21 de febrero de 2011
jueves, 17 de febrero de 2011
Movimientos de la Tierra y sus consecuencias
En esta entrada explicaré cuales son los movimientos de la tierra y sus consecuencias, como los de la Luna y las mareas. Espero que os guste:
miércoles, 16 de febrero de 2011
Componentes del Universo
El Universo está compuesto por diversos elementos, empezando de mayor a menor, estos serían lso principales:
En la siguiente presentación explicaré cada uno de los elementos del Universo. Espero que os ayude!!
- Grupos de galaxias
- Galaxias
- Nebulosas y cúmulos estelares (grupos de estrellas)
- Estrellas
- Planetas y resto de cuerpos celestes (satélites, cometas asteroides...)
En la siguiente presentación explicaré cada uno de los elementos del Universo. Espero que os ayude!!
Evolución de la concepción histórica del Universo
¿Os habéis preguntado alguna vez cuál fue el origen del universo? ¿Por qué se produjo el Big Bang? ¿Por qué el Universo está en continua expansión gracias al efecto Hubble?
En este post tengo a las respuestas a todas estas preguntas, y creo que os interesará.
Para empezar: El Universo se originó en el Big Bang. El Big Bang fue una gran explosión debido a que los protones de los átomos perdieron fuerza para chocar y encogieron. después de esto al ser los protones de los átomos todos positivos, se repelieron y querían escapar, ocasionando la gran explosión denominada Big Bang.
 Después de esto toda la materia empezó a expandirse en consecuencia de haberse repelido. A esta expansión la llamamos efecto Hubble, la cual se observó mediante el telescopio de mismo nombre y que le dio nombre a este efecto. Sé que es raro, pero mañana, las galaxias del Universo están más lejos de otras.
Después de esto toda la materia empezó a expandirse en consecuencia de haberse repelido. A esta expansión la llamamos efecto Hubble, la cual se observó mediante el telescopio de mismo nombre y que le dio nombre a este efecto. Sé que es raro, pero mañana, las galaxias del Universo están más lejos de otras. Bueno, a otro tema relacionado con esto. ¿Sabiáis qué es el geocentrismo y el heliocentrismo?
Si no lo sabéis, aquí va mi respuesta:
- El geocentrismo era la teoría de que el Sol y todos los demás astros giraban alrededor del Sol, ya que todos los planetas se veían pequeños, y todo lo pequeño gira sobre lo grande (en este caso la Tierra). También decía que la Tierra era el centro del Universo. Esta teoría la impulsó Ptolomeo
- El heliocentrismo era la teoría de que el Sol es el centro del Universo, y que todos los astros giraban alrededor de él, debido a que Eratóstenes midió el tamaño del Sol y de la Tierra. Sin embargo esta teoría la propuso Nicolás Copérnico.
El geocentrismo y el heliocentrismo tenía consecuencias sobre la manera de pensar en la gente, como podréis ver en mi presentación de diapositivas, a continuación, donde se habla del Universo y de estas dos teorías, donde creo que se explica bastante bien todo:
Incluímos un audio en el que hablamos sobre este tema los alumnos de la clase! (Algunos) :D!
Ir a descargar
Ah!, si el tema no os ha quedado claro, os dejo el siguiente enlace en el que todo está muy bien explicado:
lunes, 7 de febrero de 2011
Qué es la materia, de qué está hecha y qué no lo es.
Todos habéis oído hablar de la materia alguna vez, segurísimo. Pero, ¿habéis pensado alguna vez qué es realmente? ¿De qué está compuesta? ¿Qué no lo forma?
Si os interesa este tema, echarle un vistazo a mi presentación de diapositivas de a continuación, donde explico qué es la materia. ¡¡Espero que os ayude!!
sábado, 5 de febrero de 2011
Problema con fracciones.... Chungo, chungo..., ¿o no tanto?
Ya que hemos dado en matemáticas el tema de la fracciones, de algo nos tiene que servir, yo creo que sí, ¿no, chicos...?
Bueno, voy a poneros a continuación un problema que combine absolutamente todas las operaciones posibles con fracciones (lo que se da en 1º de Eso, claro...)
La solución la voy a tener guardada en una entrada sin publicar, y cuando ya publiquéis vuestras respuestas, colgaré el otro post con la respuesta.
Matilde tiene 20/15 de 15 euros para el cine, el cual cuesta 1/2 de 10 euros por cada persona.
Tiene que repartir el dinero entre sus tres amigos, a los que invita al cine y lo que sobre a chuches.
Al ser el día del espectador, rebajan el 10% de del precio de la entrada.
Lo que sobra de dinero a Matilde y sus amigos se lo gastan en chuches. María le da 1/3 del dinero que le sobra. Y Juan le da 1/2 de lo que le sobra.
¿Quién le ha dado más dinero a Matilde? ¿Qué fracción de dinero le queda a Matilde en forma de porcentaje?
Después del cine, María le pide a su madre dinero para comer en un restaurante de comida rápida, y le da el quíntuple de dinero que le sobraba.
miércoles, 2 de febrero de 2011
Aplicación a la orientación
Las personas hemos empezado a hacernos un montón de preguntas desde que miramos el cielo por primera vez.
Preguntas como: ¿Qué es todo eso? ¿Y qué soy yo? ¿Dónde estoy? ¿Podré viajar hacia a aquel lugar?
¿Quién hace eso?
Son muchas de las inquietudes que nos han tormentado, y a la cual hemos retribuido causas según la mentalidad de cada uno. ¿Pero sabéis cómo la gente ha empezado a viajar? Gracias a la orientación. ¿Y cómo nos hemos orientado? Fijándonos en lo único que siempre está fijo, el cielo.
Gracias al cielo hemos podido viajar, sin perdernos, sabiendo el camino que tenemos que tomar. También se ha desarrollado las matemáticas, al tener que medir distancias, religión, y un montón de cosas más.
Otra cosa muy importante "Mirando al cielo se ha dividido el tiempo". Los días de la semana, el año o los meses no surgen d ela idea de un hombre que eligió esos números, si no que los sacó de fijarse en el cielo.
A continuación, voy a mostraros una presentación de diapositivas en la que expreso esto. A parte, tenéis a vuestra disposición la página de apuntes correspondientes a este tema.
sábado, 29 de enero de 2011
La avaricia rompe el saco...
No, creo que la respuesta es no. Tenemos la ventaja de vivir en países desarrollados, en los cuales no nos faltan de nada, ni pasamos hambre. La introducción de las tecnologías modernas, la mejora del sistema sanitario, tener un techo donde dormir, tener una correcta educación, libertad de expresión, vestir la ropa adecuada, permitirnos lujos...
¿Pero de dónde se sacan todas estas cosas tan buenas...? Pues, del dinero. Sin dinero no somos nada. Sin dinero no podemos permitirnos nada. La generosidad es algo que ya no es como antes. Vas por la calle, y preguntas a un desconocido: ¿me da un euro?, es que no tengo dinero... El otro seguramente contestaría algo por el estilo: ¡Pues búscate un trabajo! Que yo también trabajo para ganar dinero...
Pero la gente no comprende que no todo el mundo tiene acceso a los mismos medios que nosotros. Las riquezas están muy mal repartidas. Vivimos en un mundo en el que "la avaricia rompe el saco". Cuanto más tenemos más queremos, sin preocuparnos por los demás. Miles de personas están muriéndose al día por no tener comida. Encima no tienen ni agua potable, ni colegios, ni hospitales. ¿Y nosotros tenemos la cara dura de querer cada vez más, y quejarnos por que no nos conformamos con nada? ¡Anda ya!
Pinchen en el siguiente enlace, ¿ a ver lo que les parece? Todo está causado por lo mismo, por el dinero.
Ahora, ¿sabéis que 1/5 de la población mundial tiene las 4/5 partes de todas las riquezas? Eso quiere decir, que si la población mundial es de 6 972 688 217, y 1/5 de 7 000 000 000 (redondeando) es de 1 400 000 000, significa que solamente esas personas tienen 4/5 de todas las riquezas del mundo. ¿Mal repartido no?
Entonces eso quiere decir que tenemos (los países desarrollados), ¡casi todo el dinero del mundo! Entonces... los demás no pueden sobrevivir, porque con el dinero se come, se viste, se duerme bajo un techo, se curan enfermedades... Que avariciosos somos, de verdad...
Es la triste realidad. Mi opinión de todo esto es sencilla, la avaricia rompe el saco, nos hace egoístas y no nos hace pensar por el que tenemos al lado.
A continuación, mostraré un montaje de diapositivas en el que intento expresar esta situación, sobre todo el desequilibrio entre los países desarrollados y subdesarrollados o Tercer Mundo:
Etiquetas:
Matemáticas,
Mujeres destacables,
Sociedad
miércoles, 26 de enero de 2011
Archaea, Bacteria y Eucarya
¿Alguna vez os habéis preguntado qué es una bacteria? ¿Qué hacen y cómo nos benefician o perjudican?
Si vuestra respuesta es sí, o tenéis curiosidad, no dudéis en mirar mi presentación de diapositivas, para informaros o resolver dudas.
A parte, tenéis los apuntes del curso correspondiente a este tema por si lo queréis o necesitáis mirar.
Si vuestra respuesta es sí, o tenéis curiosidad, no dudéis en mirar mi presentación de diapositivas, para informaros o resolver dudas.
A parte, tenéis los apuntes del curso correspondiente a este tema por si lo queréis o necesitáis mirar.
sábado, 15 de enero de 2011
¿Qué es una fracción?
En este post voy a explicaros lo que es una fracción. Es un concepto matemático, con el cual podréis aclarar vuestras dudas y los que no lo sepáis enteraros bien:
Concepto de fracción: Una fracción es la parte o las partes iguales que se cogen de una unidad o del todo.
Ejemplo: 1 = Hay un objeto o cosa que está dividida en 6 partes iguales y cojo 1.
6
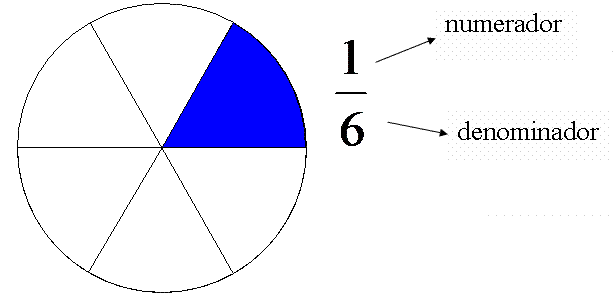
Elementos de la fracción: Cada uno de los elementos de la fracción recibe un nombre, y uno indica el número de partes que se cogen y el otro en las partes iguales en que se divide la unidad, que son los siguientes:
Numerador: Aparece encima de la línea horizontal de la fracción. Indica el número de partes iguales que se toman del denominador.
Denominador: Indica el número de partes iguales en que se divide la unidad.
Fracción =

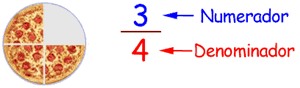

 En este caso, el numerador indica cuanto tiempo dura el compás (2 tiempos), y el denominador indica la figura que dura una parte (en este caso la negra).
En este caso, el numerador indica cuanto tiempo dura el compás (2 tiempos), y el denominador indica la figura que dura una parte (en este caso la negra).
![[atomo+de+oxigeno.gif]](https://blogger.googleusercontent.com/img/b/R29vZ2xl/AVvXsEjQeR3DKYNxYQQtgyqeQ6MKsygAHsL_GDyC7Trucs8I0TTPjVUQqAeIJPUAYwZldZ3LopRMRWH8rKDoTtx85j5rK9pVoY-o0XW3tOF4oogaQ-w46MLm4n9FyFXZAQ2r_HyOCXx9NIoAgcg/s200/atomo+de+oxigeno.gif)
Concepto de fracción: Una fracción es la parte o las partes iguales que se cogen de una unidad o del todo.
Ejemplo: 1 = Hay un objeto o cosa que está dividida en 6 partes iguales y cojo 1.
6
Elementos de la fracción: Cada uno de los elementos de la fracción recibe un nombre, y uno indica el número de partes que se cogen y el otro en las partes iguales en que se divide la unidad, que son los siguientes:
Numerador: Aparece encima de la línea horizontal de la fracción. Indica el número de partes iguales que se toman del denominador.
Denominador: Indica el número de partes iguales en que se divide la unidad.
Fracción =
Numerador
Denominador
Ejemplo : 1 = Numerador (Número partes que se toman).
2 = Denominador (Partes iguales en que se divide la unidad).
Las fracciones en la vida cotidiana: Las fracciones las utilizamos en nuestra vida diaria, casi sin darnos cuenta, son muy comunes. A continuación voy a mostrar varias situaciones en las que las utilizamos:
En las horas = Queda un cuarto de hora para que acabe la clase de matemáticas. En este caso ya estamos utilizando una fracción, ya que un cuarto es igual a esta fracción: 1
4

En las porciones de comida = Me he comido tres cuartos de la pizza. Aquí ya hemos utilizado otra fracción.
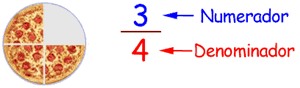
En las longitudes = Queda medio kilómetro para llegar a nuestro destino.
Para las capacidades = Queda un cuarto de litro para llenar el bidón.

En los porcentajes = Tiene un 50 % de posibilidad de éxito en la operación. Esta fracción es igual a 50
100
Aplicación de fracciones a otras asignaturas : Las fracciones se utilizan en muchas asignaturas, por no decir en todas. A continuación voy a poner un par de ejemplos:
Música: En música se utiliza mucho las fracciones, ya que los compases se indican mediante ellas (fracciones).
 En este caso, el numerador indica cuanto tiempo dura el compás (2 tiempos), y el denominador indica la figura que dura una parte (en este caso la negra).
En este caso, el numerador indica cuanto tiempo dura el compás (2 tiempos), y el denominador indica la figura que dura una parte (en este caso la negra).Ciencias Naturales: Para saber la composición de algunos elementos, como el oxígeno (O2), indica que el oxígeno está formado por una molécula con dos átomos unidos. Sería igual a la fracción 2
1 .
![[atomo+de+oxigeno.gif]](https://blogger.googleusercontent.com/img/b/R29vZ2xl/AVvXsEjQeR3DKYNxYQQtgyqeQ6MKsygAHsL_GDyC7Trucs8I0TTPjVUQqAeIJPUAYwZldZ3LopRMRWH8rKDoTtx85j5rK9pVoY-o0XW3tOF4oogaQ-w46MLm4n9FyFXZAQ2r_HyOCXx9NIoAgcg/s200/atomo+de+oxigeno.gif)
Es decir, para escribir una fórmula química escribimos los símbolos de todos los elementos que contiene esa sustancia acompañados de subíndices que indican el número de átomos de cada clase. (Fracción).
Espero que este post haya aclarado todas vuestras dudas, y si tenéis algo que decir, ¡no dudéis en comentar!
miércoles, 12 de enero de 2011
El agua como recurso y las amenazas que sufre
Cómo veréis en las siguientes diapositivas, averiguaréis las amenazas que sufre el agua, sobre todo la dulce, que es la que consumimos los humanos. En los apuntes de Ciencias Naturales (colgados en el blog) explica más detenidamente el tema, aunque yo os lo presento con unas diapositivas:
Suscribirse a:
Comentarios (Atom)