En este post, dedicado a todos los alumnos de 1º de ESO que están dando este tema, o los que están por darlo, explico qué es una ecuación, y cómo resolverla, aplicando diferentes procedimientos que voy a explicar.
Espero que os ayude :)
Primero, vamos a empezar a definir que es una ecuación, pero con mis palabras:
 Una ECUACIÓN son dos expresiones algebraicas con dos miembros, en la que se tiene que cumplir una igualdad averiguando las incógnitas, que es el nombre que reciben las letras o la parte literal de la ecuación.
Una ECUACIÓN son dos expresiones algebraicas con dos miembros, en la que se tiene que cumplir una igualdad averiguando las incógnitas, que es el nombre que reciben las letras o la parte literal de la ecuación.Es como una balanza en la que para averiguar las incógnitas hay que equilibrar la balanza, para que haya el mismo peso en ambos lados de ella.
Ejemplos:
x + 6 = 31 5 + x = 31
2x + 1 = 6x + 2 2
5(6x-3) = 6(x + 5)- x 2 + 3x = 18
Este año hemos dado las ecuaciones de primer grado, o lo que es lo mismo, ecuaciones de exponente 1.
Hay 2 procedimientos básicos para resolver 2 tipos de ecuaciones simples: La Regla de la Suma y la Regla del Producto.
Ambas consisten en equilibrar la balanza, y voy a explicarlas a continuación:
En todas las ecuaciones que os encontréis, el objetivo va a ser despejar a la x, es decir, dejarla sola para hallar su valor y poder hallar la ecuación.
En la Regla de la suma el objetivo es el siguiente, poniendo un ejemplo sencillo:
x + 6 = 18.
1º Restamos el 6 que nos "molesta" para despejar la x: x + 6 - 6
2º Pasamos la resta al otro miembro: 18 - 6
3º Realizamos las cuentas y sale el resultado: x = 12
En este caso debemos dejar a la x sola pero, para eso, hay que restar 6; pero entonces la balanza quedaría desequilibrada, así que tendríamos que restar al otro miembro también 6. Por eso decimos que una suma pasa al otro miembro restando, no por arte de magia.
Ahora, teniendo en cuenta este ejemplo, con las restas será al revés, para hacer desparecer el número al restar habrá que sumarlo. Vamos a hacer el mismo ejemplo pero restando:
x - 6 = 18
1º Sumamos el x que nos molesta. x - 6 + 6
2º Pasamos la suma al otro miembro: 18 + 6
3º Realizamos las cuentas y el resultado sale: x = 24.
Más ejemplos de la Regla de la Suma:
3x + 23 = 2x + 59
1º 3x - 2x + 23 - 23 = 59 - 23 (Este paso lo hacemos ya directamente)
2º x = 36
24 + x - 6 = 50 + 6
1º 24 - 24 + x - 6 + 6 = 50 + 6 - 24 + 6
2º x = 38
x + 7 = 7 + 12
1º x + 7 - 7 = 7 + 12 - 7
2º x = 12
Regla del Producto: Esta regla consiste en lo mismo que en la de la suma, solo que con multiplicaciones y divisiones, con la finalidad de despejar a la x. A continuación pongo un par de ejemplos para resolver con la regla del producto, con multiplicación y división:
3x = 24
4
1º Multiplicamos el denominador por 4 en el primer miembro, para quitar el denominador, pero hay que hacerlo en los 2 miembros 3x x 4 = 24 x 4
4
2º Ahora ya tenemos un resultado, pero queremos saber el valor de una x, no de 3. 3x = 96
3º Dividimos 3 entre 3 para obtener una x, y lo hacemos en el otro miembro para hallar su valor y compensar la balanza.3x = 96 x = 32
3 3
Otro ejemplo más sencillo aún:
4x = 44
1º Dividimos entre 4 para hallar el valor de una x en los dos miembros:
4x = 44 x = 11
4 4
Ahora vamos a dar la Resolución de Ecuaciones, o lo que es lo msimo, la regla práctica para resolverlas.
Vamos a dar como se resuelven ecuaciones con paréntesis y con denominadores, y mixtas. Vamos a empezar por los paréntesis:
Para resolver ecuaciones con paréntesis, seguimos el siguiente procedimiento:
1º Suprimimos los paréntesis, y para ello, hay que aplicar la propiedad distributiva.
2º Aplicamos la regla de la suma
3º Aplicamos la regla del producto
Ejemplos:
3(x + 6) + 5(2 - x) = 10 - 4(6 + 2x).
1º Suprimimos paréntesis:
3x + 18 + 10 - 5x = 10 - 24 - 8x
2º Aplicamos regla de la suma: (dejamso x en un lado y los números en otro)
3x - 5x + 8x = 10 - 24 - 18 - 10
6x = -42
3º Aplicamos la regla del producto:
6x = -42 x= -7
6x 6
Voy a poner algunas ecuaciones más de este tipo, pero ya sin explicar el proceso. ¡¡Intentar hacerlos a la misma vez y comprobar si lo tenéis bien!!
3(x - 7) = 5(x-1) - 4x
1º 3x - 21 = 5x - 5 - 4x
2º 3x- 5x + 4x = -5 + 21
3º 2x = 16 x = 8
Ahora, ya que hemos hecho ecuaciones con paréntesis, vamos a aprender hacer ecuaciones con denominadores. Los pasos son muy sencillos, y son los siguientes:
1º Suprimimos los paréntesis antes de los denominadores si hay
2º Eliminamos los denominadores.
Para ello, debemos encontrar el mcm de todos los denominadores, y cuando lo tengamos dividimos ese número entre el denominador de cada uno y lo multiplicamos por el de arriba
3º Ponemos la ecuación resultante pero suprimiendo los denominadores
4º Aplicamos la regla de la suma y del producto
Voy a poner algunos ejemplos:
1º Paréntesis
30x + 60 = 30x + 30 + 30x - 30
2 5 3
2º Eliminamos los denominadores (mcm)
450x + 900 = 180x + 180 + 300x - 300
30 30 30
3º Ecuación sin denominadores
450x + 900 = 180x + 180 + 300x - 300
4º Regla de la suma y del producto
450x - 180x - 300 = 180 - 300 - 900
270x = -1020
270x = -1020
270 270
x = -1020
270

Bueno, ya os he enseñado los procedimientos para hacer una ecuación. Ahora, ¡¡EN MARCHA!!

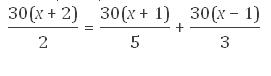
Miguel Ángel, muy buen trabajo. Me has dado alguna idea más para mi post. Se nota que te has esforzado y está genial. Yo no lo podría hacer mejor ;)
ResponderEliminarEstá perfecta pero las fracciones que has puesto no se ven bien.
ResponderEliminarAunque muy bien por resaltar lo más
¡¡Enhorabuena!!. Muy buen trabajo y muy completo. Todo está muy clarito y cuidada la presentación. Me gusta mucho cómo no pierdes en ningún momento de vista al lector dándole sugerencias de cómo pueden ir usando los distintos contenidos para aprender y sacarles provecho. Únicamente se podía completar algo con las identidades (¿cuándo una ecuación se convierte en identidad?) ó con la ec. sin solución (cuando llegamos a tonterías, ¿recuerdas?). En cualquier caso, está muy bien y se nota que has puesto tiempo, interés y empeño en el trabajo
ResponderEliminarMe encantó, me ayudaste bastante muchas gracias en verdad c: y gracias por resaltar también las partes mas importantes!
ResponderEliminarmuy bueno
ResponderEliminar:) :D
me ayudo muxo gracias tuve 10
ResponderEliminarla ultima esta mala sacaste 95
ResponderEliminar